WILLIAM T. REDMAN
I am a Research Assistant Professor in the Electrical and Computer Engineering Department at Johns Hopkins. My CV.
RECENT NEWS:
-
Starting July 1, 2026, I will be an Assistant Professor at Johns Hopkins University in the Electrical and Computer Engineering (ECE) Department and will be part of the Data Science and AI (DSAI) institute. I am actively looking to recruit graduate students and looking to work with highly motivated undergraduate students! Feel free to contact me if you think I'd be a good fit as an advisor.
-
New preprint out on using Hankel Dynamic Mode Decomposition to forecast infectious diseases in the US and Canada!
-
I am serving as an Academic Editor for PLOS Computational Biology. I'm especially interested in supporting work that explores neural computation underlying multi-agent interaction.
-
I have been invited to serve as an Action Editor for Transactions in Machine Learning Research (TMLR). I'm especially interested in supporting work in the intersection of Koopman operator theory and machine learning - feel free to reach out with any questions about submitting to TMLR!

RESEARCH
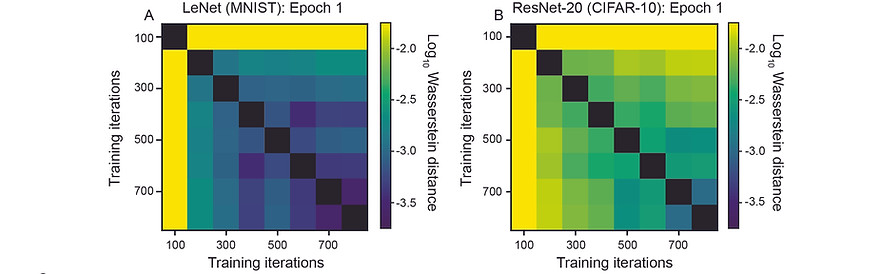
Dynamics of learning
Unlike systems neuroscientists, machine learning researchers have access to every weight, activation, and input of the networks they train. This offers great potential for understanding exactly how learning occurs in deep neural networks (DNNs). However, the complexity of modern DNN architectures make this challenging and tools for studying the high-dimensional dynamics that occur during training are lacking. With Akshunna Dogra (Imperial College London), I showed that Koopman operator theory, a data-driven dynamical systems theory framework, captures properties associated with DNN training. The inherent linearity of the Koopman operator enabled us to accelerate training, reducing training time in small DNNs by 10x-100x. See our 2020 NeurIPS paper for more details.
To obtain a complete picture of DNN training, it is necessary to have a method by which equivalent dynamics can be identified and distinguished from other, non-equivalent dynamics. To-date, such a method does not exist. Having found that we could compactly represent DNN training dynamics with Koopman operator theory, I showed, with Profs. Igor Mezic (UCSB) and Yannis Kevrekidis (JHU), that we could identify when the training of two DNNs have the same dynamics by comparing the eigenvalues associated with the Koopman operator. This enabled us to compare the early training dynamics of different convolutional neural network (CNN) architectures, as well as Transformers that do and do not undergo grokking (i.e., delayed generalization). See our 2024 NeurIPS spotlight paper for more details.

Learning of dynamics
Many of the real-world dynamical systems we care most about predicting are non-autonomous (i.e., their underlying equations change with time). To deal with this challenge, numerical approaches for Koopman operator theory are often applied along a sliding window, restricting the model to temporally local episodes. While these methods have found strong success in predicting disease, climate, and traffic, they are limited by their explicit "forgetting" of the past. This can restrict their performance in cases where dynamical regimes repeat, as the new dynamics have to be learned anew. To mitigate this, along with Prof. Igor Mezic (UCSB), I developed a new algorithm that "recalls" previous points in time where similar dynamics occurred. This is achieved by comparing Koopman representations of the current dynamics, with those saved from the past. Because this approach remembers discrete episodes, we call it "Koopman Learning with Episodic Memory". On synthetic and real-world data, we find that our method can provide a significant increase in performance, with little computational cost. See our 2025 Chaos paper for more details. I have been utilizing this approach to forecast COVID-19, RSV, and flu cases in Canada through the AI4Casting Hub challenge.
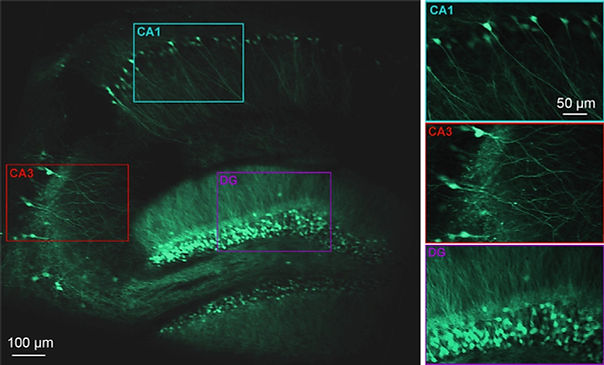
Neuroscience of spatial navigation
Spatial navigation is a critical cognitive process that is supported by the hippocampal formation. Despite decades of research, what shared and distinctive roles the subfields of the hippocampus (CA1, CA3, DG) remain unclear. This is in part due to the challenge in recording from multiple hippocampal subareas simultaneously. With my PhD advisor, Prof. Michael Goard (UCSB), I developed a novel microprism approach for optically accessing the transverse hippocampal circuit. This allowed, for the first time, 2-photon imaging of CA1, CA3, and DG simultaneously. See our 2022 eLife paper for more details.
The hippocampus is interconnected with medial entorhinal cortex (MEC), which contains neurons that exhibit periodic firing fields (grid cells). The organization of grid cells into discrete modules, where grid properties are conserved within, but not between, modules, has played a major role in guiding the fields understanding of the computations grid cells perform. However, an assumption often made in the computational neuroscience community, that grid cells in an individual module are the same (up to translation), has not been rigorously tested. Analyzing large-scale MEC recordings, we found evidence for small, but robust, heterogeneity in grid properties within a single module. We showed that this variability can be beneficial in enabling a single grid module to encode local spatial information, broadening our perspective on what computational capacity of individual grid modules is. See our 2025 eLife paper for more details.
MEC is believed to play an important role in path integration (the ability to update an estimate of position based on movement direction and speed). In many ethologically relevant settings, it is important not only to keep track of our own movements, but also the movements of others (e.g., pursuit, competition over resources). Despite this, little work has been done on understanding the computations performed by the MEC in multi-agent environments. With Prof. Nina Miolane (UCSB), I extended a recurrent neural network (RNN) model, which had previously been shown to develop properties similar to neurons in MEC when trained to perform single agent path integration. By training this extended RNN to path integrate two agents, we showed that representations different from grid cells emerged, and that the RNN learned to perform computations in a relative reference frame. Our RNN model makes direct predictions that can be tested in systems neuroscience experiments. See our 2024 NeurIPS paper for more details.

Sparse machine learning
Efforts to reduce the size and computational costs associated with modern DNNs not only provide the potential for improving efficiency, but also the potential of gaining insight on the core components that make a given DNN model successful. One such sparsification approach, iterative magnitude pruning (IMP), has shown its ability to extract subnetworks, embedded within large DNNs, that are 1-5% the size of the original network, yet can be trained to achieve similar performance. Despite its success, an understanding of how IMP discovers good subnetwork remains unclear. With Prof. Zhangyang "Atlas" Wang (UT Austin), I showed that IMP performs a function analogous to the renormalization group (RG), a tool from statistical physics that performs iterative coarse-graining to identify relevant degrees of freedom. This enabled us to leverage the rich RG literature to explain when a sparse subnetwork found by IMP on one task would generalize to another, related task. See our 2022 ICML paper for more details.
IMP has recently been shown to discover local receptive fields (RFs) in fully-connected neural networks. These local RFs are known to be good inductive biases for DNNs, and exist in primary visual cortex in the mammalian brain. How IMP identifies these local RFs has been an unresolved question, whose answer may shed light on the general success of IMP. With Profs. Sebastian Goldt (SISSA), Alessandro Ingrosso (Radboud University), and Zhangyang "Atlas" Wang (UT Austin), I provided evidence for the hypothesis that IMP maximizes the non-Gaussian statistics present in the representation of the fully-connected neural network at each round of pruning. This amplification of non-Gaussian statistics leads to stronger localization of the remaining weights. See our 2025 CPAL paper for more details.
PUBLICATIONS
PEER REVIEWED:
16) W. T. Redman, Z. Wang, A. Ingrosso, and S. Goldt, "On How Iterative Magnitude Pruning Discovers Local Receptive Fields in Fully Connected Neural Networks." Conference on Parsimony and Learning (CPAL 2025)
15) W. T. Redman, D. Huang, M. Fonoberova, and I. Mezić, Koopman Learning with Episodic Memory. Chaos Fast Track (2025)
14) W. T. Redman*, S. Acosta-Mendoza*, X.X. Wei, and M. J. Goard, Robust Variability of Grid Cell Properties Within Individual Grid Modules Enhances Encoding of Local Space. eLife (2025) (* contributed equally)
13) N. S. Wolcott, W. T. Redman, M. Karpinska, E. G. Jacobs, and M. J. Goard, "The estrous cycle modulates hippocampal spine dynamics, dendritic processing, and spatial coding." Neuron (2025)
12) W. T. Redman, J. M. Bello-Rivas, M. Fonoberova, R. Mohr, I. G. Kevrekidis, and I. Mezić, Identifying Equivalent Training Dynamics. NeurIPS Spotlight (Top 5% of accepted papers) (2024)
11) W. T. Redman, F. Acosta, S. Acosta-Mendoza, and N. Miolane, Not so griddy: Internal representations of RNNs path integrating more than one agent. NeurIPS (2024)
10) F. Acosta, F. Dinc, W. T. Redman, M. Madhav, D. Klindt, and N. Miolane, Global Distortions from Local Rewards: Neural Coding Strategies in Path-Integrating Neural Systems. NeurIPS (2024)
9) E. R. J. Levy, S. Carrillo-Segura, E. H. Park, W. T. Redman, J. Hurtado, S. Y. Chung, A. A. Fenton, "A manifold neural population code for space in hippocampal coactivity dynamics independent of place fields". Cell Reports (2023)
8) W. T. Redman, M. Fonoberova, R. Mohr, Y. Kevrekidis, and I. Mezić, "Algorithmic (Semi-)Conjugacy via Koopman Operator Theory". IEEE Conference on Control and Decision (CDC 2022)
7) W.T. Redman, N.S. Wolcott, L. Montelisciani, G. Luna, T.D. Marks, K.K. Sit, C.-H. Yu, S.L. Smith, and M.J. Goard, Long-term Transverse Imaging of the Hippocampus with Glass Microperiscopes. eLife (2022)
6) W. T. Redman, T. Chen, Z. Wang, and A. S. Dogra Universality of Winning Tickets: A Renormalization Group Perspective. International Conference on Machine Learning (ICML 2022).
5) W. T. Redman, M. Fonoberova, R. Mohr, Y. Kevrekidis, and I. Mezić, An Operator Theoretic View on Pruning Deep Neural Networks. International Conference on Learning Representations (ICLR 2022).
4) W. T. Redman, On Koopman Mode Decomposition and Tensor Component Analysis. Chaos Fast Track (2021).
3) A. S. Dogra*, and W. T. Redman* Optimizing Neural Networks via Koopman Operator Theory. Advances in Neural Information Processing Systems 33 (NeurIPS 2020) (* contributed equally)
2) W. T. Redman, Renormalization group as a koopman operator. Physical Review E Rapid Communication (2020)
1) W. T. Redman, An O(n) method of calculating Kendall correlations of spike trains. PLoS One (2019)
IN PROGRESS:
1) W. T. Redman and L. C. Mullany, Data-driven forecasting of Flu, RSV, and COVID-19 related outcomes in the United States and Canada via Hankel dynamic mode decomposition. Under review
About
I grew up in Hopewell, New Jersey, a little town outside of Princeton and Trenton. I found math class repulsive and, until I had a rather sudden change of heart my senior year, spent most of the period working on ways to avoid paying attention. Outside of research, I enjoy hiking and cycling (both of which are complicated by my innately poor sense of direction), and reading.
 |
|---|